
Berechnungen
Mengenbestimmung von Oligonucleotiden
Die Menge eines Oligonucleotids wird üblicherweise in Form seiner gesamten Optischen Dichte (OD-Wert), als Stoffmenge (nmol) oder der vorhandenen Masse (µg) angegeben. Der OD-Wert wird experimentell gemessen, die anderen Angaben werden hieraus berechnet.
Menge
OD-Wert
|
Der OD-Wert einer Probe bei einer Wellenlänge von 260 nm ist definiert als der Extinktionswert, der sich durch Absorptionsmessung der Probe in 1 ml wässriger Lösung in einer 1 cm Küvette bei der entsprechenden Wellenlänge ergibt. In der Praxis liegen OD-Werte oft außerhalb des linearen Messbereichs der UV-Spektrometer; es müssen daher verdünntere Proben quantifiziert und auf den Gesamt-OD-Wert hochgerechnet werden. Beispiel: |
Stoffmenge in nmol
Anhand des Lambert-Beer’schen Gesetzes (E = Epsilon Ɛ * C * d) kann aus der Extinktion E (OD-Wert) auf die Konzentration C und damit die Stoffmenge umgerechnet werden. Der Extinktionskoeffizient Epsilon Ɛ ist streng genommen für jede Oligonucleotidsequenz anders und müsste jeweils empirisch bestimmt werden. In guter Näherung entspricht er der Summe der Extinktionskoeffizienten der in der Sequenz vorhandenen einzelnen Nucleotide, sowie möglicher vorhandener Modifikationen.
Anhand der Sequenzdaten und des OD-Wertes lässt sich die Stoffmenge folgendermaßen berechnen:
 |
E(260nm): OD-Wert n [nmol]: Menge in nmol
A,G,C,T: Anzahl der enthaltenen Basen im Oligonucleotid
Epsilon Ɛ: Extinktionskoeffizient möglicher Modifikationen
|
Für gemischte Sequenzen ergeben sich in Abhängigkeit zur Oligolänge folgende Werte für die Stoffmenge (nmol):
| OD-Wert | Oligolänge [Anz. Nucleotide] |
|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 1 | 9,4 | 4,7 | 3,1 | 2,3 | 1,9 | 1,6 | 1,3 | 1,2 | 1,0 | 0,9 |
| 3 | 28 | 14 | 9 | 7 | 5,6 | 4,7 | 4,0 | 3,5 | 3,1 | 2,8 |
| 10 | 94 | 47 | 31 | 23 | 19 | 16 | 13 | 12 | 10 | 9 |
| 25 | 234 | 117 | 78 | 59 | 47 | 39 | 33 | 29 | 26 | 23 |
| 100 | 937 | 468 | 312 | 234 | 187 | 156 | 134 | 117 | 104 | 94 |
|
Für grobe Überschlagsrechnungen gilt also für ein gemischtes 20mer Oligonucleotid: 1 OD entspricht 5 nmol (5000 pmol). |
Oligonucleotidmenge in µg
Aus der Stoffmengenangabe (nmol) und dem Molekulargewicht des Oligonucleotids lässt sich die Oligonucleotidmenge in µg errechnen:
 |
n [µg]: Menge in µg n [nmol]: Menge in nmol
MW: Molekulargewicht
|
|
Für grobe Überschlagsrechnungen für ein gemischtes 20mer Oligonucleotid gilt ferner: 1 OD entspricht 30 µg DNA-Oligonucleotid. |
Konzentration
1. Konzentrationseinstellung auf x pmol/µl
Ein getrocknetes Oligonucleotid soll so gelöst werden, dass eine Konzentration "c" von x pmol/µl erhalten wird.
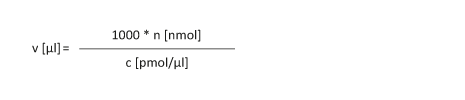 |
n [nmol]: Stoffmenge in nmol c [pmol/µl]: Konzentration
v [µl]: Volumen des Oligos
|
|
Beispiel: v [µl] = 1000 * 23 nmol / 50 pmol/µl = 460 µl Anmerkung: c [ pmol / µl ] = c [ nmol / ml ] = c [ µmol / l ] = c [ µM ] Beispiel: 248 pmol/µl = 248 nmol/ml = 248 µmol/l = 248 µM |
2. Konzentration bei Lösen in definiertem Volumen:
Ein getrocknetes Oligonucleotid wird in einem definierten Volumen Wasser gelöst, welche Konzentration ergibt sich?
 |
n [nmol]: Stoffmenge in nmol c [pmol/µl]: Konzentration
v [µl]: Volumen des Oligos
|
|
Beispiel: c[pmol/µl] = 1000 * 54 nmol / 200 µl = 270 pmol/µl |
Berechnung des Molekulargewichts
Das Molekulargewicht eines Oligonucleotids wird aus der Anzahl der einzelnen Nucleotide und evtl. vorhandener Modifikationen berechnet:
|
MWoligo (DNA) = 313,2*A + 329,2*G + 289,2*C + 304,2*T + MWmod - 62 [g/mol] MWoligo (RNA) = 329,2*A + 345,2*G + 305,2*C + 306,2*U + MWmod - 62 [g/mol] A,G,C,T: Anzahl der vorhandenen Basen im DNA-Oligo MWmod: Molekulargewicht einer Modifikation, wenn vorhanden Beispiel: MW = 313,2 * 4 + 329,2 * 4 + 289,2 * 5 + 304,2 * 8 – 62 = 6387,2 g/mol |
Schmelztemperatur
Schmelztemperatur Tm
Die Schmelztemperatur Tm eines DNA-Doppelstrangs ist als die Temperatur definiert, bei der 50 % des Doppelstrangs in einsträngiger Form vorliegt. Wichtigen Einfluss auf den Tm-Wert haben Länge, Zusammensetzung und Konzentration eines Oligonucleotids, sowie die Salzkonzentration der Lösung. Es existieren unterschiedliche, mehr oder weniger genaue Verfahren zur Vorhersage von Schmelztemperaturwerten:
|
a) Wallace-Regel (2 + 4 Regel)1 Diese für sehr kurze Oligonucleotide gültige Regel (bis ca. 15 Basen) geht von einem Beitrag von 2 Grad für jedes AT-Paar und von 4 Grad für jedes GC-Paar zur Schmelztemperatur eines DNA-Doppelstranges aus: Tm = 2°C * (A+T) + 4°C * (G+C) Diese Regel wurde für Hybridisierungen an membrangebundene Oligonucleotide erstellt und legt eine Salzkonzentration von 1 M zu Grunde. Für Lösungsexperimente sollten zu der errechneten Temperatur 8 Grad hinzuaddiert werden. b) Berechnung anhand des GC-Gehalts Die folgende auf Howly et al.2,3 zurückgehende Formel berücksichtig im Wesentlichen den GC-Gehalt und ist für lange Oligonucleotide gültig: Tm = 81,5 + 0,41 (%GC) + 16,6 log c(M+) – 500/n –0,61 (%F) –1,2 D mit :
c) Nearest-Neighbor-Verfahren Das so genannte Nearest-Neighbor-Verfahren berücksichtigt bei der Berechnung der Tm-Werte auch die sequenzabhängigen Stackingeffekte und basiert auf den thermodynamischen Daten benachbarter Nucleotidpaare. Dieses Verfahren liefert für Oligonucleotide mittlerer Länge (20 – 60 Basen) verlässliche Werte. Formel:4 Tm = [(1000 *dH) /(A + dS + R * ln (C/4))] – 273.15 + 16,6 * log c(K+) mit: |
Thermodynamische Daten:5,6
| Dinucleotide | Enthalpy dH (kcal) | Entropy dS (cal) |
|---|---|---|
| AA | -9.1 | -24.0 |
| AG | -7.8 | -20.8 |
| AC | -6.5 | -17.3 |
| AT | -8.6 | -23.9 |
| GA | -5.6 | -13.5 |
| GG | -11.0 | -26.6 |
| GC | -11.1 | -26.7 |
| GT | -6.5 | -17.3 |
| CA | -5.8 | -12.9 |
| CG | -11.9 | -27.8 |
| CC | -11.0 | -26.6 |
| CT | -7.8 | -20.8 |
| TA | -6.0 | -16.9 |
| TG | -5.8 | -12.9 |
| TC | -5.6 | -13.5 |
| TT | -9.1 | -24.0 |
|
Beispiel-Oligo: dH = -6.5 –5.6 –11.9 –5.6 –9.1 –6.5 –11.0 –11.9 –11.0 –5.6 –9.1 –9.1 – 6.5 –11.0 -5.8 -6.5 –11.0 –11.0 –11.0 –7.8 = -173.5 dS = -17.3 –13.5 –27.8 –13.5 –24.0 –17.3 –26.6 –27.8 –26.6 –13.5 –24.0 –24.0 –17.3 –26.6 –12.9 –17.3 -26.6 –26.6 –26.6 –20.8 = -430.6 Tm = (1000 x (–173.5))/ ((-10.8 –430.6 + 1.984 x ln (6.25 x 10-11)) – 273.15 + 16.6 log 50x10-3 = 60.7 Alle oben genannten Verfahren zur Schmelztemperaturberechnung beziehen Modifikationen im Oligonucleotid (z.B. Farbstoffe, Linker) nicht mit ein. |
Literatur:
1. Wallace RB, Schaffer J, Murphy RF, Bonner J, Itakura K; Nuc. Acids Res. 1979, 6, 3543.
2. Howley PM, Israel MF, Law M-F, Martin MA; J. Biological Chemistry 1979, 254, 4876.
3. Teoule R, Bazin H, Fouqué B, Roget A, Sauvaigo S; Nucleosides & Nucleotides 1991, 10, 129.
4. Rychlik W, Spencer WJ, Rhoads RE; Nuc. Acids Res. 1990, 18, 6409-6413.
5. Breslauer KJ, Frank R, Blöcker H, Marky LA; Proc. Natl. Acad. Sci 1986, 83, 3736-3750.
6. Borer PN, Dengler B, Tinoco IJ, Uhlenbeck OC; J. Mol.Biol. 1983, 86, 843-853.

